「部分文字列でない文字列」の考え方

AtCoder 版！蟻本 (初級編)の「部分文字列DP」をやっていて思ったこと。

部分文字列DP系の問題には2種類ある。

1. 部分文字列を問う問題 - ex) AOJ 2895 回文部分列
2. 部分文字列でない文字列を問う問題 - ex) ARC081-E: Don’t Be a Subsequence

1.に関してはこちらの解説が素晴らしい。完全に理解できる。 部分列 DP --- 文字列の部分文字列を重複なく走査する DP の特集

しかし、2.が難しい。考え方がどこにも解説されていない。DPの遷移式や数式は書いてあるが、「なぜその式・ロジックでいけるのか」が直感的に理解できなかった。

理解不十分なまま問題を解き進めていたら、AOJ 1392の公式解説がとてもわかりやすく理解につながった。

というわけで、以下部分文字列でない文字列を問う問題を解く上で基本となる考え方を解説する。

末尾にワイルドカードを追加し、“文字列走査グラフ”を構成する

文字列走査グラフとは私が勝手につけた名前である。問題を解くにあたり、まずは入力の文字列$S$から以下方法でグラフを構成する。なお$N=|S|$とする。

• ワイルドカード: 文字列の末尾にワイルドカード($0$とも$1$ともマッチする特殊文字)を追加する
• 頂点: 文字と文字の間を頂点とする($0$〜$N+1$の計$N+2$個の頂点が存在)
• 辺: 各頂点から、それより後で最初に現れる文字$0$の直後の頂点に遷移する有向辺を張る。文字$1$についても同様。

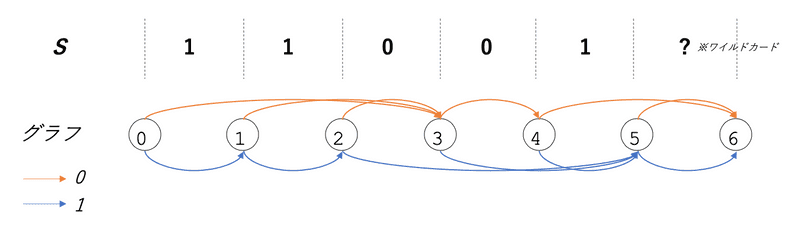
例えば$S='11001'$のときは以下のようになる。

Pythonでの実装の仕方は以下。

S = '11001'
N = len(S)

edge = [[N + 1] * 2 for _ in range(N + 1)]
# 隣接リストを N+1 で初期化
# なお、頂点N+1は辺を持たないため隣接リストには含めていない
# edge[0] = [6, 6, 6, 6, 6, 6]
# edge[1] = [6, 6, 6, 6, 6, 6]

for i in range(N - 1, -1, -1):
    for j in range(2):
        edge[i][j] = edge[i + 1][j]
    edge[i][S[i]] = i + 1
# 後ろから見ていく
# edge[0] = [3, 3, 3, 4, 6, 6]
# edge[1] = [1, 2, 5, 5, 5, 6]

さて、この文字列遷移グラフは下記2つの重要な性質を持つ。

性質1: 頂点0から各頂点への経路が、$S$のすべての部分文字列を表す

頂点0を出発してどこかの頂点に到る、その経路が部分文字列を表している。ただし頂点6は除く必要がある。

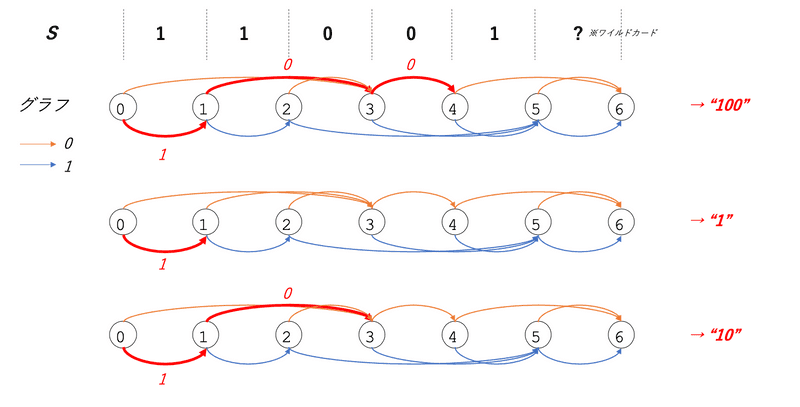
例えば、下図の赤線の経路$1→0→0$は、”$100$“という部分文字列を表す。 また、途中の$1$や$1→0$も部分文字列を表す。経路の始点は必ず頂点0であることに注意。 これらすべての経路を列挙すると$S$の”すべての”部分文字列がわかる。

性質2: 頂点$0$から頂点$6$への経路が、$S$の部分文字列でないすべての文字列を表す

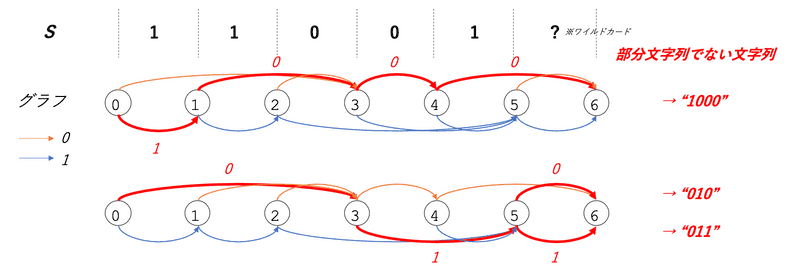
ワイルドカードを入れた理由がここにある。頂点$0$から頂点$6$への経路が、$S$の部分文字列でないすべての文字列を表すのである。

「ある頂点$a$から頂点$6$に辺$x$が存在する」$\Leftrightarrow$「頂点$a$以降に文字$x$は存在しない」

従って、頂点$0→\cdots→a→6$の経路が表す文字列は$S$の部分文字列たり得ない。なぜなら、もし部分文字列になるのであれば、頂点$a$から出ている辺$x$は頂点$6$以外を指す必要があるためである。
なお、正確を記すなら性質2は「$S$の部分文字列でない文字列のうち、“長さが$N+1$以下”のものすべてを表す」となる。

Recap

性質1: 頂点$0$から頂点$6$以外への経路が、$S$のすべての部分文字列を表す
性質2: 頂点$0$から頂点$6$への経路が、$S$の部分文字列でないすべての文字列を表す

例題: ARC081-E: Don’t Be a Subsequence

以上の知識を使って、例題としてARC081-Eを解いてみる。

問題

Aの部分列でないような最短の文字列のうち，辞書順最小のものを出力せよ．
制約
$1\leq|A|\leq2\times10^5$
$A$は英小文字のみからなる.

考え方

文字種が26あるため、各頂点から26本の辺が出るグラフを構成する。

そして、性質$2$を使うことでこの問題は以下のように言い換えられる。

頂点$0$から頂点$N+1$への最短経路のうち、辞書順最小のものを出力せよ。

最短経路を求めるには$BFS$を使えばよく、辞書順最小については各頂点にて辺を探すときに$a$の辺からアルファベット昇順に探すことで自然と満たされる。

えぇ…DPじゃないじゃん！ DP使ってもいいんですけどね。。

解答 - Python3

※残念ながらPypyじゃないと通らない。。。

from collections import deque


A = input()
N = len(A)
a = ord('a')

# edge[頂点][辺x]
edge = [[N + 1] * 26 for _ in range(N + 1)]

for i in range(N - 1, -1, -1):
    for j in range(26):
        edge[i][j] = edge[i + 1][j]
    # 文字cの直後の頂点への辺を貼る
    c = ord(A[i]) - a
    edge[i][c] = i + 1

# DP復元用。(直前の頂点, 文字)を格納する。
recon = [None] * (N + 2) 

q = deque()
q.append(0)  # 頂点0
while q:
    i = q.popleft()

    # 頂点N+1に到達したら処理終了
    if i == N + 1:  
        break
    
    # aの辺から順に処理する
    for j in range(26):
        ni = edge[i][j]
        # 頂点niに最短で到達した場合のみ次の処理を実施
        # "辞書順最小"という条件により最短でない場合は枝切りしてよい
        if recon[ni] is None:  
            recon[ni] = (i, chr(a + j))
            q.append(ni)


# reconから文字列を復元
i = N + 1
ans = []
while i > 0:
    pi, c = recon[i]
    ans.append(c)
    i = pi

print(''.join(reversed(ans)))

文字列走査グラフを制するものは部分文字列を制す

部分文字列系の問題は、この文字列走査グラフをベースに考察するのが一番簡単な気がする。境界条件の取り扱いもシンプルになる。

いずれの解法にせよ、Pythonだと文字種26の定数倍がけっこう効いてきて実行時間制約がつらい。
Numpyとか使えよって話ですかね。