2021-03-27

【Python】ABC197 解説

A - Rotate 解説

スライスを使う。

S = input()
ans = S[1:] + S[0]
print(ans)

B - Visibility

B問題にしては難しい。
マス $(X, Y)$ から $4$ 方向にそれぞれDFSを実施し、通ったマスの数を数える。

import sys
sys.setrecursionlimit(10 ** 6)


def dfs(x, y, d):
    x, y = v
    dx, dy = D[d]
    nx, ny = x + dx, y + dy
    if 0 <= nx < H and 0 <= ny < W and S[nx][ny] == '.' and path[nx][ny] == 0:
        path[nx][ny] = 1
        dfs((nx, ny), d)


H, W, X, Y = map(int, input().split())
X -= 1; Y -= 1
S = [input() for _ in range(H)]
path = [[0] * W for _ in range(H)]  # path[i][j]: マス(i, j)を通ったかどうか
path[X][Y] = 1
D = [(1, 0), (-1, 0), (0, 1), (0, -1)]  # D[]: 移動方向を定義
for i in range(4):
    dfs((X, Y), i)

ans = 0
for i in range(H):
    for j in range(W):
        ans += path[i][j]
print(ans)

C - ORXOR

C問題でORやXORが問われるのは珍しいような。

区切り位置をbit全探索する。

from itertools import product

N = int(input())
A = list(map(int, input().split()))
ans = float('inf')
for bit in product(range(2), repeat=N):  # 区切り位置を表すbit列
    if bit[-1] == 1:  # 末尾の区切りは必ず1
        xor = 0  # xor: 全体のXORの値
        sec = 0  # sec: 当該区画のORの値
        for i, a in enumerate(A):
            sec |= a  # ビット単位ORを求める
            if bit[i] == 1:  # 区画の終端の場合は、xorを更新し、secを初期化
                xor ^= sec
                sec = 0
        ans = min(ans, xor)
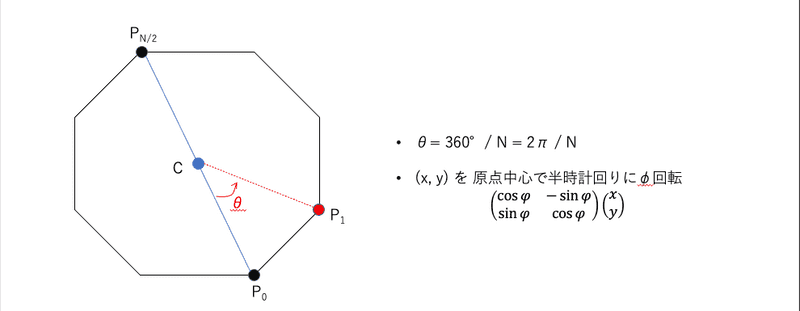
print(ans)

D - Opposite

$P_0, P_{\frac{N}{2}}$ が与えられているため、正多角形の外接円の中心 $C$ の座標がわかる。
これを利用して $C$ を中心に $p_0$ を $\frac{2\pi}{N}$ 回転させればよい。

from math import sin, cos, pi

N = int(input())
x0, y0 = map(int, input().split())  # P0
x2, y2 = map(int, input().split())


theta = 2 * pi / N  # theta: 回転させる角度（ラジアン）
Cx, Cy = (x0 + x2) / 2, (y0 + y2) / 2  # (Cx, Cy): 外接円の中心

xa, ya = x0 - Cx, y0 - Cy  # 点Cを原点に並行移動した時のP0の座標
xb, yb = xa * cos(theta) - ya * sin(theta), xa * sin(theta) + ya * cos(theta)  # (xa, ya)をθ回転
x1, y1 = xb + Cx, yb + Cy  # 原点から点Cへと並行移動
print(x1, y1)

E - Traveler

考察は易しいが実装が難しい問題。

考え方は以下。

色が小さいものから順に回収していく。
色 $i$ のものに注目すると、下記の2つのルートのどちらかが最適となる:

ルート1: 現在地 → 左端 → 右端
ルート2: 現在地 → 右端 → 左端

よって各色 $i$ 回収後に、左端・右端のそれぞれにいる場合の最小コスト・座標を管理して、次の色 $i+1$ の場合を考えればよい。

import sys

N = int(input())
ball = [[] for _ in range(N + 1)]  # ball[i]: 色iのボールの座標
for _ in range(N):
    X, C = map(int, sys.stdin.readline().split())
    C -= 1
    ball[C].append(X)
ball[N].append(0)  # 最後に座標0に戻るため、番兵として座標0のものを入れておく
for i in range(N + 1):  # 各色ごとに座標をソートする
    ball[i].sort()


INF = float('inf')

# dp[i][j]: 色iまで回収したときの最小値(左端時: j = 0, 右端時: r = 1)
dp = [[INF] * 2 for _ in range(N + 2)]  
dp[0][0] = dp[0][1] = 0


# pos[i][j]: 色iまで回収したときの現在地(左端時: j = 0, 右端時: r = 1)
pos = [[None] * 2 for _ in range(N + 2)]
pos[0][0] = pos[0][1] = 0

L, R = 0, -1  # L, R: dp配列やballにおける左端、右端を表すindex
for i in range(N + 1):
    if ball[i]:  # ボールが存在するとき
        for j in [L, R]:  # j: 現在地が左端 or 右端
            crt_cost = dp[i][j] # crt_cost: 現在値での経過時間
            crt_pos = pos[i][j]  # crt_pos: 現在地の座標

            # first, second: 回収する順番を全探索。左端→右端 or 右端→左端
            for first, second in [[L, R], [R, L]]:
                nxt_cost = crt_cost
                nxt_cost += abs(crt_pos - ball[i][first])
                nxt_cost += abs(ball[i][first] - ball[i][second])
                if nxt_cost < dp[i + 1][second]:
                    dp[i + 1][second] = nxt_cost
                    pos[i + 1][second] = ball[i][second]

    else:  # ボールが存在しないとき、単純にコピーする。参照渡しでOK。
        dp[i + 1] = dp[i]
        pos[i + 1] = pos[i]
print(min(dp[N + 1]))

##　F - Construct a Palindrome 解説AC。
うーん、これは難しい。思いつかない。。