2020-08-15
【Python】ABC175 解説
ABC175に参加しました.
結果は4完1065thでパフォーマンス1468… 実力相応かなと..
今回は全体的に考察:易, 実装:難だったように感じます.
以下, A~F問題の解説および解答例です.
A - Rainy Season
‘R’が存在するか, ‘RR’が存在するか, … と順に調べる.
S = input()
for i in range(4):
if 'R' * i in S:
ans = i
print(ans)B - Making Triangle
考え方は公式解説の通り.
候補となる3本の棒を選ぶ処理は, pythonであればitertools.combinationsを使うと簡単に実装できる.
from itertools import combinations
N = int(input())
L = list(map(int, input().split()))
cnt = 0
if N >= 3:
for edges in combinations(L, 3):
a, b, c = edges
if len(set(edges)) == 3 and a < b + c and b < c + a and c < a + b:
cnt += 1
print(cnt)C - Walking Takahashi
これは考察が難しめの問題.
考え方は以下の通り.
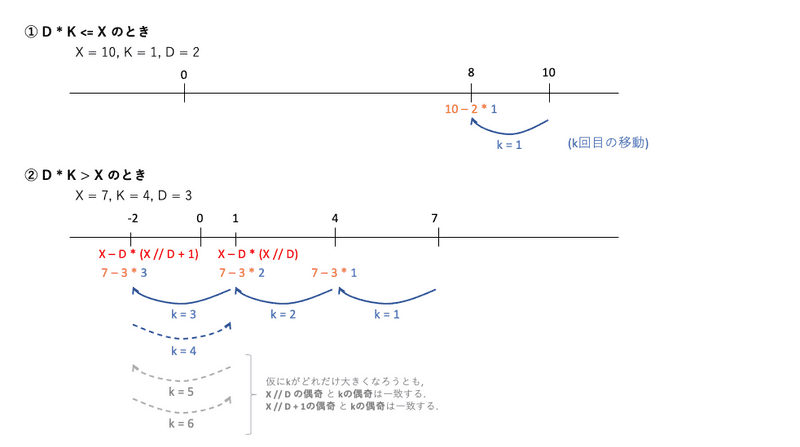
- 対称性により, は正の数() として考える.
- ① のとき
回とも動く場合が最も原点に近い. が答えとなる.
- ② のとき
解答の候補となる点は, 原点に近い0以上の点, 負の点のどちらかである. この2点を行ったり来たりする.
- では, 最終的にどちらの点に止まるのか?
- とすると, 0以上の点は, 負の点は と求めることができる.
- ここでパリティの関係より, r % 2 == K % 2 のときは0以上の点, r % 2 != K % 2のときは負の点に止まる.
X, K, D = map(int, input().split())
X = abs(X)
if K * D <= X:
ans = X - K * D
else:
r = X // D
l = X // D + 1
if r % 2 == K % 2:
ans = abs(X - D * r) # 0以上の点
else:
ans = abs(X - D * l) # 負の点
print(ans)D - Moving Piece
考察はわりと易しいと思うが, 実装が複雑. 場合分けが難しい.
- および は全て異なるという条件より, どこか�らスタートしてもスタート地点に必ず帰ってくるループとなる.
- より, すべてのスタート地点についてループ経路を求めても最悪となり, なんとか間に合いそう.
よって, 以下スタート地点として考える. 各について以下のStepを回す.
- Step1: 1番目の点 2番目の点 … s(最後の点) のループについて, 得点の累積和Sを求める.
- Step2: との大小で場合分けして, 得点の最大値を求める. 場合分けは以下の通り.
- Step2 - ケースA: のとき:
ループを1週しないため, 到達可能な点でのSの最大値が答えとなる.
- Step2 - ケースB: のとき:
S[-1]のときは1週以上するメリットがないため, 1週するまでの最大値、つまりSの最大値が答えとなる.
S[-1]のときは回れるだけ回りたいところだが, 実は1周少なく回った方が得点が高くなることがあるため, 両方の場合での得点を算出して比較する.
N, K = map(int, input().split())
P = list(map(int, input().split()))
C = list(map(int, input().split()))
ans = -float('inf')
for s in range(N):
### Step1
S = [] # 累積和S. ただし, 初項は0ではなく1回目の移動後の得点とする.
# 1回目の移動
i = P[s] - 1
S.append(C[i])
# 2回目以降の移動. スタート地点に戻ってくるまで繰り返し.
while i != s:
i = P[i] - 1
S.append(S[-1] + C[i])
### Step2: KとSの長に応じて場合分けして, 得点の最大値を求める.
# 1周未満しか移動できない場合:
if K <= len(S):
score = max(S[:K])
# 1周以上回ることができるが, ループを1周したときに得点が減る場合:
elif S[-1] <= 0:
score = max(S)
# 1週以上回ることができ, かつループを1週するごとに得点が増える場合:
else:
# ループを (K // len(S) - 1)回 廻る場合:
score1 = S[-1] * (K // len(S) - 1)
score1 += max(S)
# ループを (K // len(S))回 廻る場合:
score2 = S[-1] * (K // len(S))
r = K % len(S)
if r != 0:
score2 += max(0, max(S[:r]))
# score1 と score2 の大きい方がこの場合の得点の最大値
score = max(score1, score2)
ans = max(ans, score)
print(ans)E - Picking Goods
コンテスト終了後20分ほどでACできた.. うーん�実装力不足.
わりと典型的なDPの問題.
import sys
R, C, K = map(int, input().split())
item = [[0] * (C + 1) for _ in range(R + 1)] # dp配列と合わせるために, 0行目, 0列目を追加している.
for s in sys.stdin.readlines():
r, c, v = map(int, s.split())
item[r][c] = v
dp = [[[0] * (C + 1) for _ in range(R + 1)] for _ in range(4)]
for i in range(R + 1):
for j in range(C + 1):
for k in range(4):
here = dp[k][i][j]
# 次の行に移動する場合
if i + 1 <= R:
# 移動先のアイテムを取らない場合
dp[0][i + 1][j] = max(dp[0][i + 1][j], here)
# 移動先のアイテムを取る場合
dp[1][i + 1][j] = max(dp[1][i + 1][j], here + item[i + 1][j])
# 次の列に移動する場合
if j + 1 <= C:
# 移動先のアイテムを取らない場合
dp[k][i][j + 1] = max(dp[k][i][j + 1], here)
# 現在のkが3未満のときのみ, 移動先のアイテムを取ることが可能
if k < 3:
dp[k + 1][i][j + 1] = max(dp[k + 1][i][j + 1], here + item[i][j + 1])
ans = 0
for k in range(4):
ans = max(ans, dp[k][-1][-1])
print(ans)F - Making Palindrome
解説AC.
うーん、これは難しい…
Dijkstra法はではなくBFSで実装.
(計算量的には不利だが, Pythonではdequeを使ったBFSの方が速いことが多い.)
from collections import deque
def isPalindrome(s):
''' s: string が回文か判定する. 回文 -> True, 回文でない -> False.
'''
L = len(s)
return all(s[i] == s[L - 1 - i] for i in range(L // 2))
N = int(input())
S = []
for _ in range(N):
s, c = input().split()
S.append((s, int(c)))
path = [dict() for _ in range(2)] # 余り文字列へ到達するコスト, path[0]:左側余り, path[1]: 右側余り
q = deque()
S.sort(key=lambda x: x[1]) # コストの小さい順にソートしておくと速くなる.
for s, c in S: # 初期処理. Siを左側余り文字列と見做してキューに入れていく.
if s not in path[0] or path[0][s] > c:
path[0][s] = c
q.append((0, s, c))
INF = 10 ** 15
ans = INF
while q:
side, s0, c0 = q.popleft()
if isPalindrome(s0): # 余り文字列自体が回文のとき
ans = min(ans, c0)
else: # 余り文字列が回文でないとき, 他の文字列を追加する
for s1, c1 in S:
if side == 0:
l, r = s0, s1
else:
l, r = s1, s0
L = len(l)
R = len(r)
isCandidate = False # s1が追加可能な文字列かどうかを示すフラグ
if L > R:
if all(l[i] == r[-1 - i] for i in range(R)):
ns = l[R:]
nc = c0 + c1
nside = 0
isCandidate |= True
elif L < R:
if all(l[i] == r[-1 - i] for i in range(L)):
ns = r[:-L]
nc = c0 + c1
nside = 1
isCandidate |= True
else:
if all(l[i] == r[-1 - i] for i in range(L)):
ns = ''
nc = c0 + c1
nside = 0
isCandidate |= True
if isCandidate and (ns not in path[nside] or path[nside][ns] > nc):
path[nside][ns] = nc
q.append((nside, ns, nc))
if ans < INF:
print(ans)
else:
print(-1)関連記事最新記事
2021-05-09【Python】AtCoder - 30代社会人が始めて1年半で青色になりました
2021-04-12【Python】ABC198 解説
2021-03-27【Python】ABC197 解説
2021-03-20【Python】ABC196 解説
2021-03-13【Python】ABC195 パナソニックプログラミングコンテスト 解説