2020-06-23

【Python】ABC169 F - Knapsack for All Subsets 解説

問題

問題ページはこちら

題意

公式解説より引用.

$\{1, 2,...,N\}$ の空でない部分集合 $(T, U)$ の組であって以下の条件を満たすものは何通りありますか？
$1. T\supseteq U$
$2. U=\{x_1, x_2,...,x_k\}\text{とすると}a_{x_1}+a_{x_2}+\cdots+a_{x_k}=S$

考え方

各 $A_i$ について3つの選択肢がある

普通のナップサック問題であれば「ナップサックに入れる/入れない」の2つの選択肢だけだが, 本問では以下の3つの選択肢がある.

$T$ にも $U$ にも入れない
$T$ に入れるが, $U$ に入れない
$U$ に入れる

これらを $A$ の左から順に場合分けして数え上げていくと, 以下のような遷移をすることがわかる.

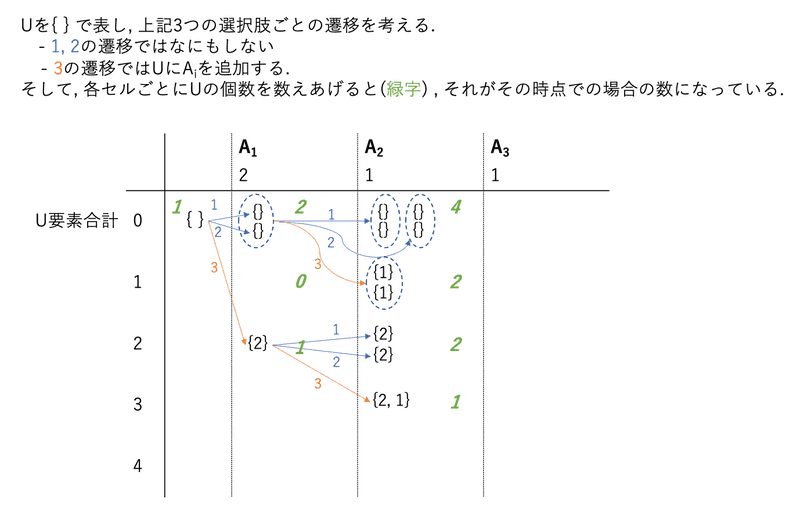
ポイントは, スタート $\rightarrow A_1$ と $A_1 \rightarrow A_2$ の遷移が独立となっている点である. つまり, 例えば $A_1 \rightarrow A_2$ を見ると $A_1$ のすべての $\{\}$ から3通りすべての遷移が行われている.
この性質によりdpで解くことができる.

解答

以上の考察により, 結局は典型的なDP問題に帰着する.

# pypyでないとTLE
N, S = map(int, input().split())
A = list(map(int, input().split()))

MOD = 998244353

# dp[i][j] := i番目までの遷移をして, Uの要素の和が j であるような場合の数
dp = [[0] * (S + 1) for _ in range(N + 1)]
dp[0][0] = 1

for i in range(N):
    ai = A[i]
    for j in range(S + 1):
        here = dp[i][j]

        # 1. TにもUにも入れない
        dp[i + 1][j] += here

        # 2. Tに入れるが, Uに入れない
        dp[i + 1][j] += here

        dp[i + 1][j] %= MOD

        # 3. Uに入れる
        if j + ai <= S:
            dp[i + 1][j + ai] += here
            dp[i + 1][j + ai] %= MOD

# 答えは, N番目まで見終わったときにUの合計=Sとなっている場合の数
print(dp[N][S])

なお, この問題では $i\rightarrow i+1$ の遷移しか無いため, dp配列を1次元で持つことができる. 当然こちらの方が速い.

# pypyでないとTLE
N, S = map(int, input().split())
A = list(map(int, input().split()))

MOD = 998244353

dp = [0] * (S + 1)  # DP配列は1次元
dp[0] = 1

for i in range(N):
    ai = A[i]
    for j in range(S, -1, -1): # 重複して数え上げないように大きい方からループする
        dp[j] = (2 * dp[j] + (j - ai >= 0) * dp[j - ai]) % MOD
 
print(dp[S])

【Python】ABC169 F - Knapsack for All Subsets 解説

目次

問題

題意

考え方

各AiA_iAi​について3つの選択肢がある

解答

各 $A_i$ について3つの選択肢がある